问题
填空题
若ab>0,且A(a,0),B(0,b),C(-2,-2)三点共线,则ab的最小值为 .
答案
16
根据A(a,0),B(0,b)确定直线的方程为 +
+ =1.
=1.
又C(-2,-2)在该直线上,故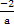 +
+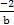 =1,
=1,
所以-2(a+b)=ab.
又ab>0,故a<0,b<0,根据基本不等式ab=-2(a+b)≥4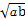 .
.
又ab>0,得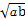 ≥4,
≥4,
故ab≥16,即ab的最小值为16.
【方法技巧】研究三点共线的常用方法
方法一:建立过其中两点的直线方程,再使第三点满足该方程.
方法二:过其中一点与另外两点连线的斜率相等.
方法三:以其中一点为公共点,与另外两点连成的有向线段所表示的向量共线.

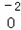 、
、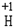 、
、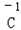 、
、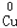 、
、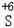 五种元素中,选择适当的元素写出下列有关物质的化学式各一种:氧化物_________,单质_________.
五种元素中,选择适当的元素写出下列有关物质的化学式各一种:氧化物_________,单质_________.