问题
填空题
已知函数f(x)＝ln x＋2x，若f(x2＋2)<f(3x)，则实数x的取值范围是________．
答案
(1,2)
由f(x)＝ln x＋2x，x∈(0，＋∞)得f′(x)＝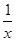
＋2xln 2>0，所以f(x)在(0，＋∞)上单调递增．又f(x2＋2)<f(3x)，
得0<x2＋2<3x，所以x∈(1,2)．
搜题请搜索小程序“爱下问搜题”
已知函数f(x)＝ln x＋2x，若f(x2＋2)<f(3x)，则实数x的取值范围是________．
(1,2)
由f(x)＝ln x＋2x，x∈(0，＋∞)得f′(x)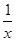＝＋2xln 2>0，所以f(x)在(0，＋∞)上单调递增．又f(x2＋2)<f(3x)，
得0<x2＋2<3x，所以x∈(1,2)．