问题
单项选择题
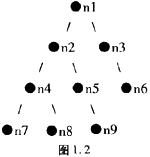
若一个二义树具有下列性质:除叶子结点外,每个结点的值都大于其左子树上的一切结点的值,并小于等于其右子树上一切结点的值。这是一棵 (50) 树。现有一个菲波那契数列an,a0 =a1=1,ak=ak-1+ak-2,k=2,3….若把a1,a2,……,a9填入具有这种性质的二叉树,一般可采用 (51) 遍历法遍历该树上全部结点,得到由结点的值组成的升序序列。对下图1.2给出的二叉树图形填入a1,……a9后,其结点n9的值为 (52) ,根结点的值为 (53) 。若欲插入a1,……a9的平均值,则应该在 (54) 增加一个结点。
A.n2与n4之间
B.n6下
C.n5与n9之间
D.n9下
答案
参考答案:D
解析: 二叉查找树是叶子结点外,每个结点的值都大于其左子树上的一切结点的值,并小于等于其右子树上一切结点的值的树。用{a1,…,a9}填充该树后,因为左子树的元素总小于根元素,右子树的元素均大于根元素,故使用中序遍历后,可得到元素的一个升序排列。填充元素后,可得到如图1.3所示二叉树:
[*]
于是n9位置的元素为a6=13,根结点n1为a7=21。{a1,…,a9}的平均值为
(1+2+3+5+8+13+21+34+55)/9=15.6.位于a6~a7间。即应在n1(a7)的左子树上,而该子树上最大结点n9,即是a6,故可将新结点加在n9下,加在n9的右子树上。
