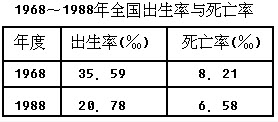
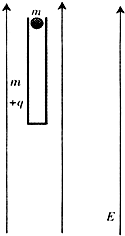
绝缘材料制成的圆柱形细管质量为m、带电荷量为+q、管长为h,管底封闭且水平,由于空间有竖直向上的匀强电场,它刚好能竖直静止.现从其管口无初速释放一个绝缘的、不带电的、质量也为m的弹性小球(直径小于管的内径,可以视为质点),不计空气对小球和细管的作用力,在小球和细管的运动或碰撞过程中,不会改变各自的带电情况,已知重力加速度为g,问:
(1)电场强度E多大?
(2)小球第一次与管底碰撞前瞬间的速度多大?
(3)小球与管底的碰撞为弹性碰撞且碰撞时间可忽略,小球第二次与管底碰前瞬间的速度多大?
(1)带电管刚好在电场中静止,则 qE=mg,得E=mg q
(2)小球在管中自由下落,小球第一次与管底碰撞前瞬间的速度为 v=2gh
(3)小球与管底发生弹性碰撞,两者组成的系统动量守恒,得 mv=mv1+mv2
机械能守恒得
mv2=1 2
m1 2
+v 21
m1 2
(式中v1、v2分别是小球与管底碰撞后的速度) v 22
解方程得 v1=0,v2=v=2gh
两者碰后管向下做匀速运动,小球做自由落体运动,直到它们再第二次相碰.
设第一次碰后到第二次相碰的时间为t,则
对小球有 s=
gt21 2
对管有 s=v2t
解得:t=2v2 g
故小球第二次跟管底相碰时的速度为
=gt=2v2=2v /2 2gh
答:
(1)电场强度E是
.mg q
(2)小球第一次与管底碰撞前瞬间的速度是
.2gh
(3)小球与管底的碰撞为弹性碰撞且碰撞时间可忽略,小球第二次与管底碰前瞬间的速度是2
.2gh