问题
问答题
假设市场上只有两个寡头垄断厂商，其成本函数分别为TC1=
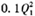+20Q1+100 000，TC2=
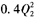+32Q2+20 000。这两个厂商生产同质的产品，其市场需求函数为Q=4 000-10P。现两个厂商同意建立一个卡特尔，以求他们的总利润最大。试求：
(1)总产量、价格及两厂商的产量分别是多少
(2)成立卡特尔之后，两个寡头垄断厂商的总利润是多少
答案
参考答案：(1)在卡特尔中，为求利润最大，必须使行业(即两厂商加总)的边际成本MC等于行业边际收益，并且各厂商根据各自的边际成本等于行业边际成本和边际收益的原则分配产量。根据已知条件，可求得MC1、MC2和MR，但不知MC。在卡特尔中，有MC1=MC2=MR=MC。
根据已知条件，MC1=0.2Q1+20，MC2=0.8Q2+32。
由此可得，Q1=5MC-100，Q2=1.25MC-40。
两式相加得Q=6.25MC-140，故MC=0.16Q+22.4
由已知条件可得行业反需求函数为[*]
从而可得总收益[*]
根据MR=MC，可求得Q=1 049，进一步地，可以求得P=295，MC=190
从而有Q1=5MC-100=850，Q2=1.25MC-40=199
即总产量为1049，价格为295，厂商1的产量为850，厂商2的产量为199。
(2)π1=P·Q-TC1=295×850-(0.1×8502+2.0×850+100 000)=61 500
π2=P·Q-TC2=295×199-(0.4×1992+32×199+20 000)=16 497
π=π1+π2=77 997。即成立卡特尔后，两个寡头垄断厂商的总利润为77 997。