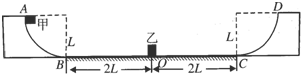
如图所示的凹形场地,两端是半径为L的光滑
圆弧面,中间是长为4L的粗糙水平面.质量为3m的滑块乙开始停在水平面的中点O处,质量为m的滑块甲从光滑圆弧面顶端A处无初速度滑下,进入水平面内并与乙发生碰撞,碰后以碰前一半的速度反弹.已知甲、乙与水平面的动摩擦因数分别为μ1、μ2,且μ1=0.25,μ2=1 4
.甲、乙的体积大小忽略不计.求:μ1 2
(1)甲与乙碰撞前的速度;
(2)碰后瞬间乙的速度;
(3)甲、乙在O处发生碰撞后,刚好不再发生碰撞,则碰后甲乙通过的路程之比为多少,甲、乙停在距B点多远处.
(1)设甲到达O处与乙碰撞前的速度为v甲,由动能定理可得:
m甲gL-μ1m甲g•2L=
m甲v甲2-0,1 2
解得:v甲=
;gL
(2)设碰撞后甲、乙的速度分别为v甲′、v乙′,以甲的初速度方向为正方向,由动量守恒定律得:
m甲v甲=m甲v甲′+m乙v乙′,
由题意知:v甲′=-
v甲=-1 2
,gL 2
解得:v乙′=
v甲=1 2
;gL 2
(3)由于μ1=2μ2,所以甲、乙在水平面上运动的加速度满足:a甲=2a乙,
设甲在水平地面上通过的路程为s1、乙在水平地面上通过的路程为s2,
由速度位移公式:v甲′2=2a甲s1,v乙′2=2a乙s2,
即:
=s1 s2
…①1 2
由于甲、乙刚好不再发生第二次碰撞,所以甲、乙在同一地点停下.有以下两种情况:
第一种情况:甲返回时未到达B时就已经停下,此时有:s1<2L,
而乙停在甲所在位置时,乙通过的路程为:s2=2L+2L+s1=4L+s1,
因为s1与s2不能满足①,因而这种情况不能发生.
第二种情况:甲、乙分别通过B、C冲上圆弧面后,返回水平面后相向运动停在同一地点,所以有:s1+s2=8L…②
①②两式得:s1=
L或s2=8 3
L,16 3
即小车停在距B为:△L=s1-2L=
L;2 3
答:(1)甲与乙碰撞前的速度为
;gL
(2)碰后瞬间乙的速度
;gL 2
(3)通过的路程之比为1:2,甲、乙停在距B点
L处.2 3
