问题
解答题
某公司为一家制冷设备厂设计生产某种型号的长方形薄板，其周长为4m．这种薄板须沿其对角线折叠后使用．如图所示，ABCD(AB＞AD)为长方形薄板，沿AC折叠后AB′交DC于点P.当△ADP的面积最大时最节能，凹多边形ACB′PD的面积最大时制冷效果最好．
(1)设AB＝xm，用x表示图中DP的长度，并写出x的取值范围；
(2)若要求最节能，应怎样设计薄板的长和宽？
(3)若要求制冷效果最好，应怎样设计薄板的长和宽？
答案
（1）y＝2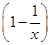
，1＜x＜2.（2）当薄板长为
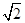m，宽为(2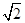－)m时，节能效果最好．（3）当薄板长为
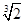m，宽为(2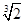－)m时，制冷效果最好．
(1)由题意，AB＝x，BC＝2－x.
因x＞2－x，故1＜x＜2.设DP＝y，则PC＝x－y.
因△ADP≌△CB′P，故PA＝PC＝x－y.
由PA2＝AD2＋DP2，得
(x－y)2＝(2－x)2＋y2y＝2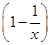，1＜x＜2.
(2)记△ADP的面积为S1，则
S1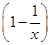＝ (2－x)＝3－
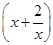≤3－2，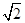
当且仅当x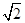＝∈(1，2)时，S1取得最大值．
故当薄板长为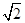m，宽为(2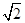－)m时，节能效果最好．
(3)记多边形ACB′PD的面积为S2，则
S2＝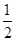
x(2－x)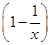＋(2－x)＝3－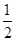
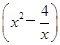，1＜x＜2.
于是S2′＝－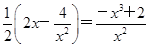
＝0x＝.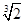
关于x的函数S2在(1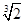，)上递增，在(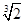，2)上递减．所以当x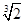＝时，S2取得最大值．
故当薄板长为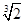m，宽为(2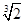－)m时，制冷效果最好
。
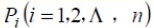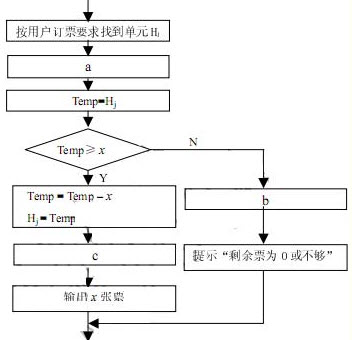
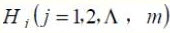单元存放某日某车次的剩余票数，Temp 为Pi 进程的临时工作单元，x 为某用户的订票张数。初始化时系统应将信号量S 赋值为 （23） 。Pi 进程的工作流程如下，若用 P 操作和 V 操作实现进程间的同步与互斥，则图中 a、b 和 c 应分别填入 （24） 。