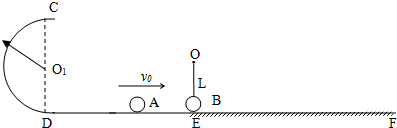
如图所示，质量为3m的小球B用长度为L=r的细线悬挂于O点，小球B位

问题问答题

如图所示，质量为3m的小球B用长度为L=r的细线悬挂于O点，小球B位于水平轨道DE与EF的分界点E，但对接触面无压力，DE段光滑，EF段粗糙，与两个小球的动摩擦因数均为μ=0.5，另一个质量为m的小球A以初速度v₀2

5gr

与B发生正碰后反弹，从D点进入竖直放置的半径为r的光滑半圆轨道CD，恰好到达最高点C，离开C点后落在轨道DE的G点（图中未画出），A球、B球均视为质点，重力加速度用g表示，求：

（1）碰后A球的速度v_A

（2）A球落点G点与D点的水平距离x

（3）如细线能承受的最大拉力F_m=16mg，碰后，悬挂B球的细线是否断开？如不能断开，求出B球上摆的最大高度h；如能断开，求出B球在水平轨道EF上运动的最大距离S．

答案

（1）A球刚好通过最高点，由牛顿第二定律得

mg=m

vC2

解得：vC=

对A球碰后运动至C过程，由机械能守恒得

mv_A²=

mv_C²+mg2r

解得v_A=

5gr

（2）A球平抛过程有

2r=

gt2

x=v_Ct

解得x=2r

（3）A、B两球相碰过程，由动量守恒得

mv₀=m（-v_A）+3mv_B

B球在最低点由牛顿第二定律得

F-3mg=3m

vB2

所以有：vB=

5gr

，F=18mg

因为F＞F_m=16mg所以细线断

B球在水平面上做匀减速运动，由动能定理得

-μ3mgs=0-

3mv_B^{2
解得s=5r
答：（1）碰后A球的速度为
5gr
；
（2）A球落点G点与D点的水平距离为2r；
（3）碰后，悬挂B球的细线会断开，B球在水平轨道EF上运动的最大距离为5r．}