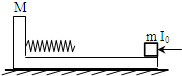
如图所示,质量为M=3kg、长度为L=1.2m的木板静止在光滑水平面上,其左端的壁上有自由长度为L0=0.6m的轻弹簧,右端放置一质量为m=1kg的小物块,小物块与木块间的动摩擦因数为μ=0.4,今对小物块施加一个水平向左的瞬时冲量I0=4N•s,小物块相对于木板向左运动而压缩弹簧使弹性势能增大为最大值Emax,接着小物块又相对于木板向右运动,最终恰好相对静止于木板的最右端,设弹簧未超出弹性限度,并取重力加速度为g=10m/s2.求:
(1)当弹簧弹性势能最大时小物块速度v;
(2)弹性势能的最大值Emax及小物块相对于木板向左运动的最大距离Lmax.
(1)由动量定理得I0=mv0
弹簧弹性势能最大时物块与木板的速度相同,则由动量守恒定律得 mv0=(m+M)v
于是可解得:v=1m/s.
(2)由动量守恒定律和功能关系得
mv0=(m+M)u
物块相对于木板向左运动过程:
mv1 2
=20
(m+M)v2+μmgLmax+Emax 1 2
物块相对于木板向右运动过程:
mv1 2
=20
(m+M)u2+2μmgLmax1 2
可解得:Emax=3J,Lmax=0.75m.
答:
(1)当弹簧弹性势能最大时小物块速度v是1m/s;
(2)弹性势能的最大值Emax为3J,小物块相对于木板向左运动的最大距离Lmax是0.75m.
