问题
问答题
设f(0)=0,f’(x)∈(0,1),证明
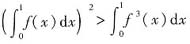 .
.
答案
参考答案:本题考查微积分不等式的证明.题目给出积分形式的研究对象,要求用导数工具进行讨论,是典型考题.
证明如下:将积分的上限变量化,作辅助函数[*],则
[*]
再令[*],则
G’(x)=2f(x)=2f(x)f’(x)=2f(x)[1-f’(x)],
由于f(0)=0,f’(x)∈(0,1),所以当x>0时,f(x)>0,故
G’(x)=2f(x)[1-f’(x)]>0,
G(x)单调增加,则G(x)>G(0)=0,于是F’(x)>0,F(x)单调增加,则F(x)>F(0)=0,即
[*]
