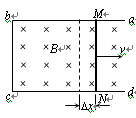
（1）如图1所示，固定于水平面上的金属框架abcd，处在竖直向下的匀强磁场中。金属棒MN沿框架以速度v向右做匀速运动。框架的ab与dc平行，bc与ab、dc垂直。MN与bc的长度均为l，在运动过程中MN始终与bc平行，且与框架保持良好接触。磁场的磁感应强度为B。
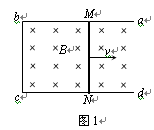
a. 请根据法拉第电磁感应定律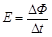
，推导金属棒MN中的感应电动势E；
b. 在上述情景中，金属棒MN相当于一个电源，这时的非静电力与棒中自由电子所受洛伦兹力有关。请根据电动势的定义，推导金属棒MN中的感应电动势E。
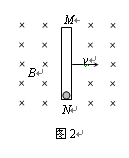
（2）为进一步研究导线做切割磁感线运动产生感应电动势的过程，现构建如下情景：如图2所示，在垂直于纸面向里的匀强磁场中，一内壁光滑长为l的绝缘细管MN，沿纸面以速度v向右做匀速运动。在管的N端固定一个电量为q的带正电小球（可看做质点）。某时刻将小球释放，小球将会沿管运动。已知磁感应强度大小为B，小球的重力可忽略。在小球沿管从N运动到M的过程中，求小球所受各力分别对小球做的功。
（1）见解析 （2）洛伦兹力做功为0，管的支持力做功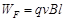
题目分析：（1）
如图1所示，在一小段时间Dt内，金属棒MN的位移
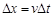（2分）
这个过程中线框的面积的变化量
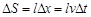（1分）
穿过闭合电路的磁通量的变化量
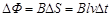（1分）
根据法拉第电磁感应定律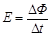 
（1分）
解得 
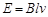（1分）
如图2所示，棒向右运动时，电子具有向右的分速度，受到沿棒向下的洛伦兹力
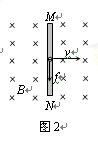
，f即非静电力（2分）
在f的作用下，电子从M移动到N的过程中，非静电力做功
（2分）
根据电动势定义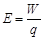 
（1分）
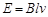解得 （1分）
（2）小球随管向右运动的同时还沿管向上运动，其速度如图3所示。小球所受洛伦兹力f合如图4所示。将f合正交分解如图5所示。 （2分）
小球除受到洛伦兹力f合外，还受到管对它向右的支持力F，如图6所示。
洛伦兹力f合不做功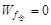 
（2分）
沿管方向，洛伦兹力f做正功 
垂直管方向，洛伦兹力
是变力，做负功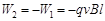 
（2分）
由于小球在水平方向做匀速运动，则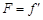 
（1分）
因此，管的支持力F对小球做正功 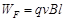（1分）
说明：用其它方法计算管的支持力F对小球所做功，只要过程、结果正确，可得4分。