问题
问答题
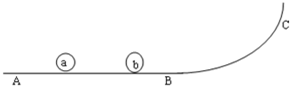
现有光滑的轨道ABC,其中AB部分是水平的,上面有大小相等两球a和b,b球静止,a球质量是2kg,b球4kg,a球正以速度υ0=7m/s向右运动,与b球发生了碰撞.已知碰撞时间是t=0.01s,b球被碰后沿BC曲面上升的最大高度H=0.8m.
求:
(1)b球给a球的平均作用力多大(g=10m/s2);
(2)通过计算说明碰撞过程中a、b组成的系统机械能是否守恒?
答案
对b球被碰后沿BC曲面上升的过程运用动能定理得:
0-
mbvb2=-mbgh1 2
解得:vb=4m/s
在碰撞过程中动量守恒,根据动量守恒定律得:
mav0=mava+mbvb
解得:va=-1m/s
对a球运用动量定理得:
Ft=mava-mav0
解得:F=-1600N
即b球给a球的平均作用力为1600N;
(2)碰撞前ab的动能之和为:Ek1=
mav02=49J1 2
碰撞后ab的动能之和为:Ek2=
mava2+1 2
mbvb2=33J1 2
因为Ek1>Ek2
所以碰撞过程中a、b组成的系统机械能不守恒.
答:(1)b球给a球的平均作用力为1600N;
(2)碰撞过程中a、b组成的系统机械能不守恒.