问题
问答题
如图,Q为一个原来静止在光滑水平面上的物体,其DB段为一半径为R的光滑圆弧轨道,AD段为一长度为L=R的粗糙水平轨道,二者相切于D点,D在圆心O的正下方,整个轨道位于同一竖直平面内.物块P的质量为m(可视为质点),P与AD间的动摩擦因数μ=0.1,物体Q的质量为M=2m,重力加速度为g.
(1)若Q固定,P以速度v0从A点滑上水平轨道,冲至C点后返回A点时恰好静止,求v0的大小和P刚越过D点时对Q的压力大小.
(2)若Q不固定,P仍以速度v0从A点滑上水平轨道,求P在光滑圆弧轨道上所能达到的最大高度h.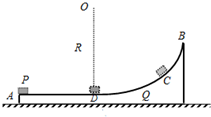
答案
(1)P从A到C又返回A的过程中,由动能定理有
-μmg•2L=0-
m1 2
①v 20
将L=R代入①解得
v0=
②2gR 5
若P在D点的速度为vD,Q对P的支持力为FD,由动能定理和牛顿定律有
-μmgL=
m1 2
-v 2D
m1 2
③v 20
根据牛顿第二定律得
FD-mg=m
④v 2D R
联立解得
FD=1.2mg⑤
由牛顿第三定律可知,P对Q的压力大小也为1.2mg.
(2)当PQ具有共同速度v时,P达到的最大高度h,由动量守恒定律有
mv0=(m+M)v⑥
由功能关系有
m1 2
=μmgL+v 20
(m+M)v2+mgh⑦1 2
联立解得
h=
R1 30
答:(1)若Q固定,P以速度v0从A点滑上水平轨道,冲至C点后返回A点时恰好静止,v0的大小是
,P刚越过D点时对Q的压力大小是1.2mg.2gR 5
(2)若Q不固定,P仍以速度v0从A点滑上水平轨道,P在光滑圆弧轨道上所能达到的最大高度h是
R.1 30
