问题
解答题
已知函数f(x)＝xk＋b(其中k，b∈R且k，b为常数)的图象经过A(4,2)、B(16,4)两点．
(1)求f(x)的解析式；
(2)如果函数g(x)与f(x)的图象关于直线y＝x对称，解关于x的不等式：g(x)＋g(x－2)>2a(x－2)＋4.
答案
（1）f(x)＝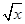
.
（2）①若a≤2，则不等式的解集为{x|x>2}；
②若a>2，则不等式的解集为{x|x>a}．
(1)
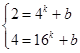⇒b＝0，k＝
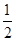⇒f(x)＝.
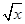(2)设M(x，y)是曲线y＝g(x)上任意一点，由于函数g(x)与f(x)的图象关于直线y＝x对称，所以M(x，y)关于直线y＝x的对称点M′(y，x)必在曲线y＝f(x)上，所以x＝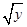
，即y＝x2，所以g(x)＝x2(x≥0)，于是
g(x)＋g(x－2)>2a(x－2)＋4
⇔
⇔
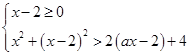
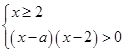
①若a≤2，则不等式的解集为{x|x>2}；
②若a>2，则不等式的解集为{x|x>a}．
