问题
问答题
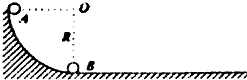
如图所示,足够长光滑水平轨道与半径为R的光滑四分之一圆弧轨道相切.现从圆弧轨道的最高点由静止释放一质量为m的弹性小球A,当A球刚好运动到圆弧轨道的最低点时,与静止在该点的另一弹性小球B发生没有机械能损失的碰撞.已知B球的质量是A球质量的k倍,且两球均可看成质点.
(1)若k已知且等于某一适当的值时,A、B两球在水平轨道上经过多次没有机械能损失的碰撞后,最终恰好以相同的速度沿水平轨道运动.求该速度的大小;
(2)若第一次碰撞结束的瞬间,A球对圆弧轨道最低点压力刚好等于碰前其压力的一半,求k的可能取值:
答案
(1)设最终两球的速度大小为v,根据机械能守恒可得:
mgR=
mv2+1 2
kmv2,1 2
解得:v=
.2gR k+1
(2)设A球到达圆弧轨道最低点时速度为v0,则:
mv02=mgR1 2
设此时A球对轨道压力为N,则:N-mg=mv02 R
设碰撞后A球的速度大小为v1,对轨道的压力为N1,B球的速度为v2,选v0的方向为正,则:
mv0=kmv2±mv1,
mv02=1 2
mv12+1 2
kmv22,1 2
N1-mg=m
N1=v12 R
N1 2
代入数值解上述方程组可得:k=3或k=
.1 3
答:(1)该速度的大小为v=
.2gR k+1
(2)k的可能取值为3或
.1 3
