问题
填空题
若存在实常数k和b，使得函数f(x)和g(x)对其定义域上的任意实数x分别满足：f(x)≥kx＋b和g(x)≤kx＋b，则称直线l：y＝kx＋b为f(x)和g(x)的“隔离直线”．已知h(x)＝x2，φ(x)＝2eln x(其中e为自然对数的底数)，根据你的数学知识，推断h(x)与φ(x)间的隔离直线方程为________．
答案
y＝2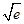
x－e
容易观察到h(x)和φ(x)有公共点(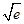，e)，又(x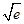－)2≥0，即x2≥2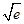x－e，所以猜想h(x)和φ(x)间的隔离直线为y＝2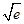x－e，下面只需证明2eln x≤2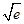x－e恒成立即可，构造函数λ(x)＝2eln x－2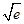x＋e.由于λ′(x)＝
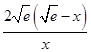(x>0)，即函数λ(x)在区间(0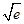，)上递增，在(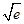，＋∞)上递减，故λ(x)≤λ(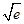)＝0，即2eln x－2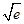x＋e≤0，得2eln x≤2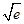x－e.故猜想成立，所以两函数间的隔离直线方程为y＝2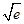x－e.