设f(x)在(a,+∞)内有二阶导数,且f(a+1)=0,
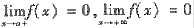 ,试证:在(α,+∞)内至少有一点ξ使f"(ξ)=0.
,试证:在(α,+∞)内至少有一点ξ使f"(ξ)=0.
参考答案:(1)已知f(a+1)=0,若在(a+1,+∞)[*](a,+∞)内f(x)=0,则f(x)=0(x∈(a+1,+∞)),则对任意ξ∈(a+1,+∞)[*](a,+∞),都有f"(ξ)=0,结论成立.
(2)若在(a+1,+∞)[*](a,+∞)内f(x)≠0,则至少存在x0∈(a+1,+∞),使f(x0)≠0,无妨设此时f(x0)>0.
由于f(x)在[a+1,+∞)连续,且f(a+1)=0,[*]0,而f(x0)>0,根据连续函数介值定理,必有x1,x2,使a+1<x1<x0,x0<x2<+∞,使f(x1)<f(x0),f(x2)<f(x0)分别在[x1,x0],[x0,x2]上用拉格朗日中值定理,存在ξ1∈(x1,x0),ξ2∈(x0,x2)使[*]
因为f(x)二阶可导,故f’(x)在[ξ1,ξ2]上连续,依连续函数零值定理,存在ζ∈(ξ1,ξ2)[*](a+1,+∞),使f’(ζ)=0.
再补充定义f(a)=[*]f(x)=0,且f(a+1)=0,则f(x)在[a,a+1]连续,依罗尔定理存在η∈(a,a+1)使f’(η)=0.
而可导函数f’(x)在[η,ζ][*](a,+∞)上连续,且f’(η)=f’(ζ)=0,再用罗尔定理,存在ξ∈(η,ζ)[*](a,+∞),使f"(ξ)=0.
解析:[考点] 利用微分中值定理做证明
