问题
多项选择题
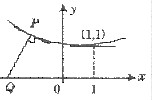
设上半平面上一条凹曲线(如下图所示),其上任一点P(x,y)处的曲率等于此曲线在该点的法线PQ长度的倒数(Q是法线与x轴的交点),而且曲线在点(1,1)处的切线与x轴平行,求此曲线方程.
答案
参考答案:记曲线为y=f(x),由于曲线为凹弧,即y">0,故曲率
[*]
又因为曲线过点(x,f(x))的法线方程为
X-x+f’(x)(Y-f(x))=0.
它与x轴交点Q的横坐标为X0=x+f’(x)f(x),所以线段PQ长度为
[*]
[*]
于是该曲线满足的微分方程为
[*]
即 [*]
方程不显含x,令p=y’,则[*],方程化为[*],则[*],其解为A+pB=cyB,代入初始条件,y(A)=A,p|x=A=0得c=A.
即pB=y’B=yB-A,从而[*],分离变量后,代入初始条件无论右端取正号,负号,其解均为[*]
解析:[考点] 利用曲率列方程,求曲线
