问题
解答题
已知直线l1:x+a2y+1=0和直线l2:(a2+1)x-by+3=0(a,b∈R).
(1)若l1∥l2,求b的取值范围;
(2)若l1⊥l2,求|ab|的最小值.
答案
(1)(-∞,-6)∪(-6,0]
(2)2
解:(1)因为l1∥l2,
所以-b-(a2+1)a2=0,
即b=-a2(a2+1)=-a4-a2
=-(a2+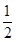 )2+
)2+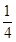 .
.
因为a2≥0,所以b≤0.
又因为a2+1≠3,所以b≠-6.
故b的取值范围是(-∞,-6)∪(-6,0].
(2)因为l1⊥l2,
所以(a2+1)-a2b=0.
显然a≠0,所以ab=a+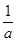 ,
,
|ab|=|a+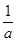 |≥2,
|≥2,
当且仅当a=±1时等号成立,
因此|ab|的最小值为2.
