问题
问答题
设A=(aij)n×n是秩为n的n阶实对称矩阵,Aij是|A|中元素aij的代数余子式(i,j=1,2,…,n)二次型
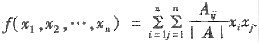
(1)记X(x1,x2,…,xn)T,试写出二次型f(x1,x2,…,xn)的矩阵形式.
(2)判断二次型g(X)=XTAX与f(X)的规范形是否相同,并说明理由.
答案
参考答案:(1)r(A)=n,故A是可逆的实对称矩阵,于是(A-1)T=(AT)-1=A-1,即A-1是实对称矩阵,亦即[*]是实对称的,从而A*是实对称矩阵,由此即知Aij=Aji(i,j=1,2,…,n)于是有
[*]
因此,二次型f的矩阵表示为XTA-1X,其二次型矩阵为A-1.
(2)因为A,A-1都是可逆的实对称矩阵,且(A-1)TAA-1=(A-1)TE=(AT)-1=A-1,所以A与A-1合同,于是g(X)与f(X)有相同的规范形.
解析:[考点] 二次型的矩阵表示及规范形
