问题
解答题
某工厂生产一种产品的原材料费为每件40元，若用x表示该厂生产这种产品的总件数，则电力与机器保养等费用为每件0.05x元，又该厂职工工资固定支出12500元．
(1)把每件产品的成本费P(x)(元)表示成产品件数x的函数，并求每件产品的最低成本费；
(2)如果该厂生产的这种产品的数量x不超过3000件，且产品能全部销售，根据市场调查：每件产品的销售价Q(x)与产品件数x有如下关系：Q(x)＝170－0.05x，试问生产多少件产品时，总利润最高？(总利润＝总销售额－总成本)
答案
（1）P(x)＝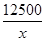
＋40＋0.05x，每件产品成本的最小值为90元
（2）生产650件产品时，总利润最高，最高总利润为29750元
解：(1)P(x)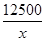＝＋40＋0.05x，
由基本不等式得
P(x)≥2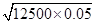
＋40＝90.
当且仅当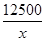＝0.05x，即x＝500时，等号成立．
∴P(x)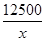＝＋40＋0.05x，每件产品成本的最小值为90元．
(2)设总利润为y元，则
y＝xQ(x)－xP(x)＝－0.1x2＋130x－12500＝－0.1(x－650)2＋29750.
当x＝650时，ymax＝29750.
答：生产650件产品时，总利润最高，最高总利润为29750元．