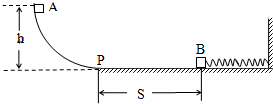
如图所示,质量为m=1kg的滑块A从光滑圆弧h=0.9m处由静止开始下滑,轻弹簧的一端固定,另一端与滑块B相连,B静止在水平导轨上,B滑块与A滑块的质量相等,弹簧处在原长状态.滑块从P点进入水平导轨,滑行S=1m后与滑块B相碰,碰撞时间极短,碰后A、B紧贴在一起运动,但互不粘连.已知最后A恰好返回水平导轨的左端P点并停止.滑块A和B与水平导轨的滑动摩擦因数都为μ=0.1,g=10m/s
求:
(1)滑块A与滑块B碰撞前的速度
(2)滑块A与滑块B碰撞过程的机械能损失
(3)运动过程中弹簧最大形变量x.
(1)令A、B质量皆为m,A刚接触B时速度为v1(碰前),由动能定理,有
mgh=
mv021 2
-μmgs=
mv12-1 2
mv021 2
解得:v1=4m/s
(2)A、B碰撞过程中动量守恒,令碰后A、B共同运动的速度为v2,有mv1=2mv2
解得:v2=2m/s
A、B碰撞过程机械能损失
△E=
mv12-1 2
(m+m)v22=4J1 2
(3)碰后A、B先一起向左运动,接着A、B一起被弹回,在弹簧恢复到原长时,设A、B的共同速度为v3,在这过程中,由动能定理,有:-μ•(2m)g•(2x)=
•(2m)v32-1 2
•(2m)v221 2
此后A、B开始分离,A单独向右滑到P点停下,由动能定理有
-μmgs=0-
mv321 2
解得:v3=
m/s,x=0.5m2
答:(1)滑块A与滑块B碰撞前的速度为4m/s;
(2)滑块A与滑块B碰撞过程的机械能损失为4J;
(3)运动过程中弹簧最大形变量为0.5m.
