问题
填空题
已知∠AOB=45°,点P在∠AOB的内部,P1与P关于OB对称,P2与P关于OA对称,则P1,O,P2三点构成的三角形是______.
答案
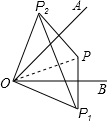
如图,连接OP,
∵P1与P关于OB对称,P2与P关于OA对称,
∴OP=OP1=OP2,∠BOP1=∠BOP,∠AOP2=∠AOP,
∴∠P1OP2=∠BOP1+∠BOP+∠AOP2+∠AOP=2(∠BOP+∠AOP)=2∠AOB,
∵∠AOB=45°,
∴∠P1OP2=2×45°=90°,
∴P1,O,P2三点构成的三角形是等腰直角三角形.
故答案为:等腰直角三角形.
