问题
解答题
已知直线l：3x-y+3=0，求：
(1)点P(4，5)关于l的对称点；
(2)直线x-y-2=0关于直线l对称的直线方程．
答案
解：设P(x，y)关于直线l：3x-y+3=0的对称点为P′(x′，y′)，
∵kPP′·kl=-1，即
×3=-1，①
又PP′的中点在直线3x-y+3=0上，
∴3×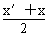
-
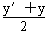+3=0，②
由①②得
，
(1)把x=4，y=5代入③及④得x′=-2，y′=7，
∴P(4，5)关于直线l的对称点P′的坐标为(-2，7)；
(2)用③④分别代换x-y-2=0中的x，y，
得关于l的对称直线方程为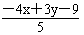
-
-2=0，
化简得7x+y+22=0。