问题
问答题
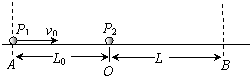
如图所示,在光滑绝缘水平面上,不带电的绝缘小球P2静止在O点.带正电的小球P1以速度v0从A点进入AB区域.随后与P2发生正碰后反弹,反弹速度为
v0.从碰撞时刻起在AB区域内加上一个水平向右,电场强度为E0的匀强电场,并且区域外始终不存在电场.P1的质量为m1,带电量为q,P2的质量为m2=5m1,A、O间距为L0,O、B间距为L=2 3
,已知4L0 3
=qE0 m1
.4v02 3L0
(1)求碰撞后小球P1向左运动的最大距离及所需时间.
(2)判断两球能否在OB区间内再次发生碰撞.
答案
(1)碰撞后P1以速度v1=
v0向左做匀减速直线运动,设最大距离为s,由运动学公式有2 3
v12=2as①
v1=at②
由牛顿第二定律有
qE0=m1a③
又
=qE0 m1
④4v02 3L0
联立解得
s=
L0⑤1 6
所需时间t=
⑥L0 2v0
(2)设碰后P2速度为v2,以v0方向为正方向,由动量守恒:
m1v0=m1(-
v0)+m2v2⑦2 3
设P1、P2碰撞后又经△t时间在OB区间内能再次发生碰撞,
P1位移为s1,P2位移为s2,由运动学公式,有
s1=-
v0△t+2 3
a△t2⑧1 2
s2=v2△t⑨
s1=s2⑩
联立解得
s2=
<L=L0 2
两球能在OB区间内再次发生碰撞.4L0 3
答:(1)碰撞后小球P1向左运动的最大距离为
.所需时间为L0 6
.L0 2v0
(2)两球能在OB区间内再次发生碰撞.
