问题
问答题
在所有周长等于6的直角三角形中，求出斜边最小的三角形．
答案
参考答案：
[考点点击] 本题考查最值的应用．
[要点透析] 设直角三角形的两直角边为x，y，斜边为z，则有
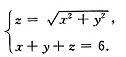
构造拉格朗日函数L(x，y)=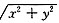
+λ(x+y+z-6)=(1+λ)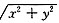+λ(x+y-6)，
解方程组
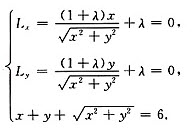
当λ=-1时，方程组的前两个式子都不成立，故λ≠-1．
解得
由于实际情况必存在斜边最小值，故当直角三角形的两直角边长均为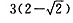
时，斜边最小．