问题
问答题
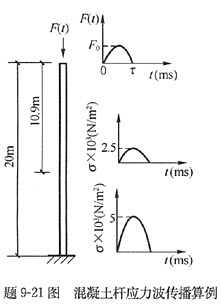
已知一根长20m,截面0.2m×0.2m均匀混凝土杆，弹性模量E＝3.2×1010N/m2，质量密度ρ＝2400kg/m3，杆下端固定，杆上端受到一半正弦脉冲力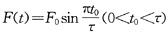
激励，F0＝100N,τ＝5ms。据此即可求出t＝3.0ms、5.5ms时杆中最大应力及传播深度(忽略—切阻尼)。
答案
参考答案：
(1)由弹性模量公式求得应力波沿杆传播的波速C为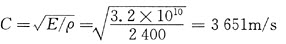
。
(2)当t1＝3.0ms时，应力波传播至深度z1
z1＝Ct1＝3651×0.003＝10.95m
当t2＝5.5ms时，应力波传播至深度z2
z2＝Ct2＝3651×0.0055＝20m
所以t2＝5.5ms，应力波正好传播至杆件的固定端端部，下行压力波传至固定端反射为压力波，应力加倍，此时杆中应力最大，σ＝2500×2＝5000N/m2。