设g(x)在(-∞,+∞)连续,对任意实数x,有g(x+1)=g(x),且
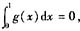 ,而f(x)在[0,1]上有连续的导数,记
,而f(x)在[0,1]上有连续的导数,记
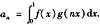 试证:级数
试证:级数
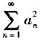 收敛。
收敛。
参考答案:g(x)是以T=1为周期的连续周期函数,满足[*]是以T=1为周期的可导函数,由连续周期函数积分性质知
[*]
[*]
由于G(X)在(-∞,+∞)连续,以T=1为周期,从而有界,即存在常数M1>0使
|G(X)|≤M1,于是|G(nx)|≤M1 (x∈(-∞,+∞))
又f’(x)在[0,1]连续,故有界,即存在常数M2>0,使
|f’(x)|≤M2(x∈[0,1])
由(*)式,有
[*]
依正项级数比较判别法知[*]收敛,
解析:[考点] 级数收敛性的判定
