问题
问答题
矩阵
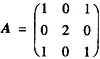，矩阵B=(kE+A)2，k为实数。
求对角矩阵Λ，使B与A相似。
答案
参考答案：AT=A，即A是实对称矩阵。
[*]
A的特征值为λ1=0，λ2=λ3=2，于是存在正交矩阵P，使
[*]
因为BT=[(kE+A)2]T=(kE+A)T(kE+A)T
=(kE+AT)2=(kE+A)2=B，
即B也是实对称矩阵，且
B=[P(kE)PT+PΛ1PT]2
=[P(kE+Λ1)PT][P(kE+Λ1)PT]=P(kE+Λ1)2PT
于是PTBP=P-1BP=(kE+Λ1)2
[*]
即B与A相似。