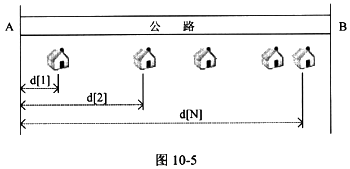
【说明】 在一条农村公路的一边稀疏地分布着房子,其分布如图10-5所示。某电信公司需要在某些位置放置蜂窝电话基站,由于基站的覆盖范围是6公里,因此必须使得每栋房子到某个基站的直线距离不超过6公里。为简化问题,假设所有房子在同一直线上,并且基站沿该直线放置。现采用贪心策略实现用尽可能少的基站覆盖所有的房子。
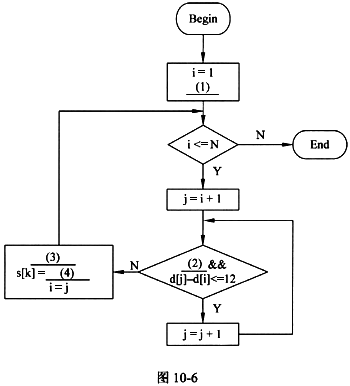
 实现贪心算法的流程如图10-6所示,请填充其中空白并计算该算法的时间复杂度,其中: 1.d[i](1≤i≤N)表示第i个房子到公路A端的距离,N表示房子的总数,房子的编号按照房子到公路A端的距离从小到大进行编号。 2.s[k]表示第k(k≥1)个基站到公路A端的距离,算法结束后k的值为基站的总数。
实现贪心算法的流程如图10-6所示,请填充其中空白并计算该算法的时间复杂度,其中: 1.d[i](1≤i≤N)表示第i个房子到公路A端的距离,N表示房子的总数,房子的编号按照房子到公路A端的距离从小到大进行编号。 2.s[k]表示第k(k≥1)个基站到公路A端的距离,算法结束后k的值为基站的总数。
 该算法的时间复杂度为 (5) 。
该算法的时间复杂度为 (5) 。
参考答案:
解析:(1)k=0
(2)j<=N,或其等价形式
(3)k=k+1,或其等价形式
(4)d[i]+6,或其等价形式
(5)O(N),或O(n)
[分析]:
该问题可以建模为如图10-7所示,其中直线表示房子所在的直线,实心正方形表示房子。问题是要求如何在该直线上布局机站,使其能覆盖所有的房子,并且所用机站的数量要尽可能的少。这是一个通过进行一系列选择求最优解的问题。

分析该问题,发现其具有最优子结构,并且具有贪心选择性质,故该问题可以用贪心算法来求解。算法思想:问题的规模为N。从第一个房子(最左端)开始布局机站,把第一个机站放置在该房子右方的6公里处,这时该机站会覆盖从第一个房子到其右方 12公里的直线的长度上的所有房子,假设覆盖了N1个房子。此时问题规模变成了N-N1。把第一个机站覆盖的房子去掉,再从N-N1中选择第一个(最左端)房子开始布局机站,将第二个机站放置在该房子右方的6公里处。依此布局,直到覆盖所有的房子。
图10-8是问题解的模型,其中直线表示房子所在的直线,实心正方形表示房子,实心圆形表示机站,虚线圆以对应机站为圆心,直径为机站的覆盖范围,即对应机站的覆盖范围。

算法中包含两个循环,但实际上只是遍历所有房子一次,故算法复杂度是O(N)。

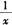 的()。
的()。