[A] Convenient packaging
[B] Health and wellness
[C] Skeptical customers
[D] Enormous markets
[E] Soaring sales
[F] Trendy drink
In the last 40 years the bottled water industry has gone from a business prospect that few took seriously, to a global industry worth billions of pounds. The commodity itself remains simple. The way we think about it has changed fundamentally. Water is natural, pure and sourced at minimal cost. Its real value lies in its marketing and branding. "I think bottled water is the most revealing substance for showing us how the global capitalist market works today," says Richard Wilk, professor of anthropology at Indiana University. "In a sense we’re buying choice, we’re buying freedom. That’s the only thing that can explain why you would pay money for a bottle of something that you can otherwise get for free. "
41. ______
Through a confection of advertising and marketing, bottled water has become one of the biggest success stories in the modern food and beverage industry. "The demand for bottle water has grown exponentially in the last few decades," says Dr. Peter Gleick, author of Bottled and Sold. "It’s doubled, it’s doubled again and it’s doubled again. And the bottle water companies see enormous markets not just in the rich countries but also in the poorer countries. "
No actual variety
Some people think that bottled water is the high point of global capitalism, particularly the people in the bottled water business. "I think bottled water actually represents a kind of caricature of the global economy. It provides people in the developed world with 20 or 30 varieties of something for which there is no actual variety," says Charles Fishman, author of The Big Thirst.
42. ______.
At the beginning there really was no variety and the bottled water phenomenon began with one brand. Perrier (佩绿雅,矿泉水品牌) was a triumph of advertising, creating a brand that was to define a generation. At the heart of the campaign to make the brand popular was Richard Wheatley, of the Leo Burnett advertising agency between 1979 and 1994. "Perrier popularised bottled water," he says. "It made it acceptable, more than acceptable, it made it... desirable. " But it was not an instant success. When Perrier UK was looking to increase its sales in the early 1970’s, it faced a skeptical public. Many questioned why anyone would buy water when you could get it free from the tap.
43. ______.
Faced with obstacles, Perrier turned to advertising with a campaign that was to change our consumer landscape for ever. The campaign was a marketing coup and sales went through the roof from 12 million bottles in 1980 to 152 million by the end of the decade. Perrier was no longer just a bottle of water. The marketing and advertising teams had established a crucial emotional link between the product and the consumers. "Perrier became a badge," says Michael Bellas, chairman of the Beverage Marketing Corporation. "When you held a Perrier bottle up, it said something about yourself, it said you were sophisticated, you understood what was happening in the world. It was a perfect beverage for the young and coming business executives, the trend-setters. "
44. ______.
In an age of instant gratification, still water in portable bottles provided what people needed, exactly when they needed it. "People in general are more and more time pressed," says Mr. Fishman. "We don’t cook our own meals any more, we eat prepared foods of all kinds. And there’s nothing more appealing than a bottle of cold water at a moment when you’re really thirsty. But I think bottled water is one of those products that on many occasions when people buy it, what they’re buying isn’t the water so much as the bottle. That is the package and the convenience at that moment. "
45. ______.
When people bought this convenience, what they were really buying was Polyethylene Terephthalate, or PET, the single most important innovation in the industry’s history. Strong, shatterproof and a highly valued form of polyester, PET is a by-product of the oil industry. It is now utilised in the packaging of everything from pharmaceuticals and soap, to ready meals. In years to come, the environmental impact of PET would haunt the industry and raise questions about its very survival, but in the 1990s this was a revolution. According to Mr. Bellas it was behind the subsequent incredible growth of the industry. "Starting with the introduction of the small premium PET waters, the category started to explode," says Mr. Bellas. "The bottled water industry before PET on the list of all beverage categories was number seven. With the advent of PET, water jumped to the number two spot, behind carbonated soft drinks. "
By branding and marketing water, bottled water has been transformed from something that many of us took for granted into a product that now makes billions for global multinational companies.
45()
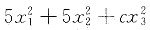 -2x1x2+6x1x3-6x2x3的秩为2,求参数c及此二次型对应矩阵的特征值.
-2x1x2+6x1x3-6x2x3的秩为2,求参数c及此二次型对应矩阵的特征值.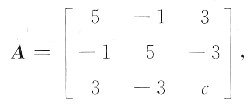
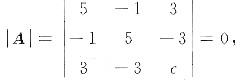 解得c=3.
解得c=3.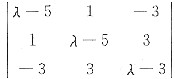 =λ(λ-4)(λ-9),
=λ(λ-4)(λ-9),