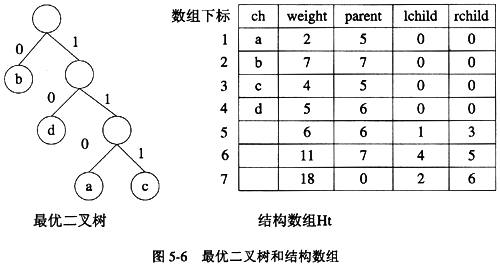
【预备知识】 ①对给定的字符集合及相应的权值，采用哈夫曼算法构造最优二叉树，并用结构数组存储最优二叉树。例如，给定字符集合{a，b，c，d}及其权值2、7、4、5，可构造如图5-6所示的最优二叉树和相应的结构数组Ht(数组元素Ht[0]不用)。

结构数组Ht的类型定义如下： #define MAXLEAFNUM 20 struct node{ char ch;/*当前节点表示的字符，对于非叶子节点，此域不用*/ int weight; /*当前节点的权值*/ int parent; /*当前节点的父节点的下标，为0时表示无父节点*/ int lchild,rchild; /*当前节点的左、右孩子节点的下标，为0时表示无对应的孩子节点*/ }Ht[2*MAXLEAFNUM]; ②用“0”或“1”标识最优二叉树中分支的规则是：从一个节点进入其左(右)孩子节点，就用“0”(“1”)标识该分支(示例见图5-6)。 ③若用上述规则标识最优二叉树的每条分支后，从根节点开始到叶子节点为止，按经过分支的次序，将相应标识依次排列，可得到由“0”、“1”组成的一个序列，称此序列为该叶子节点的前缀编码。例如图5-6所示的叶子节点a、b、c、d的前缀编码分别是110、0、111、10。 【函数5-6说明】 函数void LeafCode(int root，int n)的功能是：采用非递归方法，遍历最优二叉树的全部叶子节点，为所有的叶子节点构造前缀编码。其中形参root为最优二叉树的根节点下标，形参n为叶子节点个数。 在构造过程中，将Ht[P].weight域用做被遍历节点的遍历状态标志。 【函数5-6】 char **Hc; void LeafCode(int root, int n) /*为最优二叉树中的n个叶子节点构造前缀编码，root是树的根节点下标*/ {int i,p=root,cdlen=0;char code[20];Hc=(char**)maloc((n+1)*sizeof(char*)); /*申请字符指针数组*/for(i=1;i＜=p;++i) Ht[i].weight=0; /*遍历最优二叉树时用做被遍历节点的状态标志*/while(p){/*以非递归方法遍历最优二叉树，求树中每个叶子节点的编码*/ if(Ht[p].weight==0){/*向左*/ Ht[p].weight=1; if(Ht[p].lchild !=0){ p=Ht[p].lchild; code[cdlen++]=’0’; }else if(Ht[p].rchild==0){ /*若是叶子节点，则保存其前缀编码*/ Hc[p]=(char *)malloc((cdlen+1)*sizeof(char)); (1) ; strcpy(Hc[p],code); } }else if(Ht[p].weight==1)(/*向右*/ Ht[p].weight=2; if(Ht[p].rchild !=0){ p=Ht[p].rchild; code[edlen++]=’1’; } }else { /*Ht[p].weight==2，回退*/ Ht[p].weight=0; p= (2) ; (3) ; /*退回父节点*/ }}/*while结束*/ } 【函数5-7说明】 函数void Decode(char *buff,int root)的功能是：将前缀编码序列翻译成叶子节点的字符序列，并输出。其中形参root为最优二叉树的根节点下标，形参buff指向前缀编码序列。 【函数5-7】 void Decode(char *buff,int root) {int pre=root,p;while(*buff !=’\0’){ p=root; while(p !=0){/* 存在下标为p的节点*/ pre=p; if( (4) )p=Ht[p].lchild; /*进入左子树*/ else p=Ht[p].rchild; /*进入右子树*/ buff++; /*指向前缀编码序列的下一个字符*/ } (5) ; printf("%c",Ht[pre].ch);} }