问题
问答题
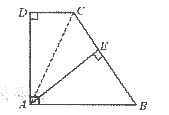
如图,在直角梯形ABCD中,AB∥CD,AD⊥DC,AB=BC,且AE⊥BC.

(1)求证:AD=AE;
(2)若AD=8,DC=4,求AB的长.
答案
参考答案:
(1)连接AC.
∵AB∥CD.
∴∠ACD=∠BAC.
∵AB=BC。
∴∠ACB=∠BAC,
∴∠ACD=∠ACE.
又∵AD⊥DC,AE⊥BC,
∴∠D=∠AEC=90°,
∴△ADC≌△AEC,
∴AD=AE.
(2)由(1)知:AD=AE,DC=EC.
设AB=x,则BE=x-4,AE=8.
在Rt△ABE中∠AEB=90°,
由勾股定理得:82+(x-4)2=x2,
解得:x=10,
∴AB=10.
