问题
填空题
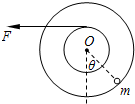
半径分别为r和2r的两个质量不计的圆盘,共轴固定连结在一起,可以绕水平轴O无摩擦转动,大圆盘的边缘上固定有一个质量为m的质点,小圆盘上绕有细绳.开始时圆盘静止,质点处在水平轴O的正下方位置.现以水平恒力F拉细绳,使两圆盘转动,若两圆盘转过的角度θ=
时,质点m的速度最大,则恒力F=______;若圆盘转过的最大角度θ=π 6
则此时恒力F=______.π 3
答案
以水平恒力F拉细绳,使两圆盘转动,若两圆盘转过的角度θ=
时,质点m的速度最大,此时力矩平衡,故:π 6
F?r=mg?2rsin30°
解得:F=mg;
根据能量守恒定律得
F?
r=mg?2rcosπ 3
解得F=π 3 3mg π
本题答案是:mg,
.3mg π
