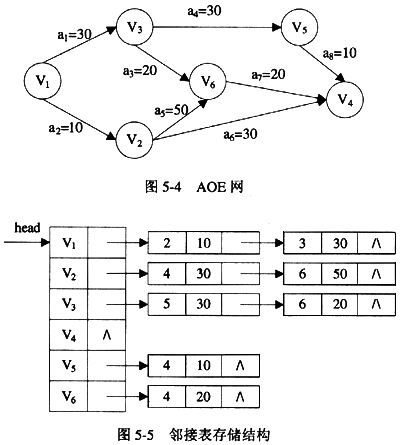
【说明】 函数int Toplogcal(LinkedWDigraph G)的功能是对图G中的顶点进行拓扑排序，并返回关键路径的长度。其中图G表示一个具有n个顶点的AOE网，图中顶点从1～n依次编号，图G的存储结构采用邻接表表示，其数据类型定义如下： typedef struct Gnode{ /*邻接表的表节点类型*/int adjvex; /*邻接顶点编号*/int weieht; /*弧上的权值*/stract Gnode *nextarc; /*指示下一个弧的节点*/ }Gnode; typedef struct Adjlist{/*邻接表的头节点类型*/char vdata; /*顶点的数据信息*/struct Gnode *Firstadj; /*指向邻接表的第一个表节点*/ }Adjlist; typedef struct LinkedWDigraph{ /*图的类型*/int n,e; /*图中顶点个数和边数*/struct Adjlist *head; /*指向图中第一个顶点的邻接表的头节点*/ }LinkedWDigraph; 例如，某AOE网如图5-4所示，其邻接表存储结构如图5-5所示。
int Toplogical(LinkedWDigraph G) { Gnode *p; int j,w,top=0; int *Stack,*ve,*indegree; ve=(int*)malloc((G.n+1)*sizeof(int)); indegree=(int*)malloc((G.n+1)*sizeof(int)); /*存储网中各顶点的入度*/ Stack=(int*)malloe((G.n+1)*sizeof(int));/*存储入度为0的顶点的编号*/ if(!ve||!indegree||!Stack)exit(0); for(j=1;j＜=G.n;j++){ve[j]=0;indegree[j]=0; }/*for*/ for(j=1;j＜=G.n;j++){ /*求网中各顶点的入度*/ p=G.head[j].Firstadj; while(p){ (1) ; p=p-＞nextarc; }/*while*/ }/*for*/ for(j=1;j＜=G.n;j++) /*求网中入度为0的顶点并保存其编号*/if(!indegree[j])Stack[++top]=j; while(top＞0){w= (2) ;printf("%c",G.head[w].vdata);p=G.head[w].Firstadj;while(p){ (3) ; if(!indegree[p-＞adjvex]) Stack[++top]=p-＞adjvex; if( (4) ) ve[p-＞adjvex]=ve[w]+p-＞weight; p=p-＞nextarc;}/*while*/ }/*while*/ return (5) ; }/*Toplogical*/
参考答案：
解析：(1) indegree[p-＞adjvex]++，及其等价形式 (2) Stack[top--]，及其等价形式 (3) indegree[p-＞adjvex]--，及其等价形式 (4) ve[w]+p-＞weight＞ve[p-＞adjvex]，及其等价形式 (5) ye[w)，及其等价形式
[分析]： 本题考查AOE网络及其拓扑排序和关键路径，做题前需要先弄清楚图G的存储结构。 根据注释，空(1)所在for循环用来统计AOE网中各顶点的入度。根据入度的定义及题中AOE网的存储结构，当p不为NULL时，应将p-＞adjvex对应的顶点的入度加1。又数组 indegree正是用来存储各顶点入度的，从紧接着的用来求入度为0的顶点的for循环可看出， indegree数组有效下标是从1到G.n，而顶点的编号正好也是从1开始，故空(1)应填 indegree[p-＞adjvex]++。 各顶点入度统计结束后，收集入度为0的顶点并将其编号保存在栈Stack(数组模拟)中，栈顶指针为数组下表top。 接下来根据各顶点入度进行拓扑排序输出。 空(2)是给变量w赋值，紧接着将w对应的信息输出，根据拓扑排序算法，此处是选择一个入度为0的顶点输出。Stack栈存储的正是入度为0的顶点编号，故空(2)应填Stack[top--]。注意top指向的栈顶，因此不能写成Stack[--top]；另外，这里是出栈操作，不能写成Stack[top]。 根据拓扑排序算法，接下来需要将变量w对应的顶点的所有出边删除，即将对应的顶点的入度减1。类似空(1)，空(3)应填indegree[p-＞adjvex]--。接着判断相应顶点的入度是否为0，为0时将其入栈。 空(4)比较难确定，因程序中并未说明ve数组的用途，注意到函数需要返回关键路径的长度，而至此尚无任何相关语句。因此可以断言ve数组正是为了计算关键路径长度而设置的。关键路径是指从开始到结束点的最长路径，所以只要保证每到一个顶点vx，ve[vx]中存储的都是从开始顶点到vx的最长路径(即顶点vx的最早发生时间)即可。故空(4)应填“ve[w]+p-＞weight＞ve[p-＞adjvex]”。这样，空(5)很容易得出应填“ve[w]”。