问题
问答题
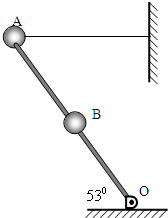
如图所示,一根长为l的轻质直杆,可绕光滑转轴O自由转动,在其中点、上端分别固定质量均为m的小球B、A,小球A用水平绳系住,使杆与水平面成53°角.
(1)当小球A用水平绳系住时,求杆对小球A的作用力的大小时,某同学解答如下:设杆对小球的作用力的大小为F,对小球受力分析,小球受到重力、绳的水平拉力,及沿杆方向的弹力,因小球受共点力作用平衡,由F合=0,求得杆对球的作用力,由此所得结果是否正确?若正确,请求出结果;若不正确,请说明理由并给出正确的解答.
(2)当释放绳子时,求小球A将要到地面时的速度大小.
答案
(1)不正确,因杆对小球的作用力不是沿杆方向;
设杆对小球的作用力在水平方向分量为Fx,竖直方向为Fy 绳对小球的拉力为T,则
Fy=mg ①
Fx=T ②
对小球及杆整体,以O为转动轴,由力矩平衡条件得
Tlsin53°=mglcos53°+mg
lcos53° ③1 2
由③式得T=
mg,所以杆对小球的作用力大小为F=9 8
=
+F 2x F 2y
mg;145 8
(2)由机械能守恒,设小球A的速度为v1,小球B的速度为v2;
v1=2v2
由④⑤得v2=
,所以A的速度为:v1=2 3gl 5
;4 3gl 5
答:(1)由此所得结果不正确,杆对小球A的作用力的大小为
mg;145 8
(2)当释放绳子时,小球A将要到地面时的速度大小为
.4 3gl 5
