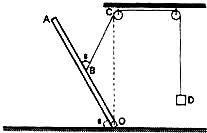
如图所示,质量为m、长为L的均匀细杆OA,一端通过光滑铰链固定在地面O处,在细杆中点B处系一根细绳,细绳绕过两个光滑定滑轮后悬挂着物体D,物体D的质量为细杆质量的1/3,D离滑轮距离足够远.在外力F的作用下使细杆与地面保持夹角θ为60°,此时细绳CB与杆的夹角也为60°(如图所示).已知细杆绕O点转动的动能表达式为Ek=
mL2ω2,m表示杆的质量,L表示杆的长度,ω表示杆转动的角速度.求:1 6
(1)外力F的最小值.
(2)撤去外力F后,细杆从图示位置到绕O点罢到地面前的过程中,系统(指细杆和物体D)重力势能的变化量.
(3)撤去外力F后,细杆绕O点转到地面的瞬间,物体D的速度大小.
(1)要使F最小,F必须作用于A点,且方向垂直于杆斜向上.如图.
根据力矩平衡条件得:FL+T
sin60°=mgcos60°L 2 
又T=
mg1 3
代入解得 F=
mg=0.11mg3- 3 12
(2)撤去外力F后,细杆从图示位置到绕O点罢到地面前的过程中,物体D的重力势能增大,杆的重力势能减小,
由图可知,细杆重心下降了
L,物体D上升了3 4 L 2
则△EP=
mg•1 3
-mgL 2
L=3 4
mgL=-0.27mgL2-3 3 12
即系统的重力势能减小了0.27mgL.
(3)设细杆着时角速度为ω,B点着地时速度为vB,物体D的速度为vD,则
vB=ω•
vD=vBsinθL 2
根据系统机械能守恒得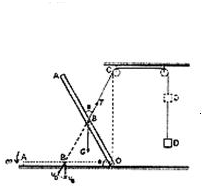
mL2ω2+1 6
×1 2
m1 3
=-△EPv 2D
代入解得vD=0.5gL
答:(1)外力F的最小值为0.11mg.
(2)撤去外力F后,细杆从图示位置到绕O点罢到地面前的过程中,系统重力势能的变化量为-0.27mgL.
(3)撤去外力F后,细杆绕O点转到地面的瞬间,物体D的速度大小为vD=0.5
.gL
