问题
问答题
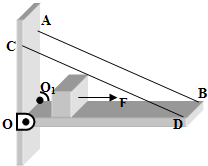
如图所示,质量不计、长度1米的轻质薄木板BDOO1被铰链和轻质细绳AB、CD水平地固定在竖直墙壁上,AB、CD与水平木板之间的夹角为30度,一重量为10牛顿的木块(可视为质点)置于木板的左端,木块与木板之间的摩擦系数为0.2,现对物块施加一水平向右的拉力F,F=7N,两根绳子各自能承受的最大拉力为9N,问:
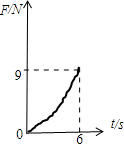
(1)定量画出绳中的拉力T随时间t的变化规律;
(2)是否有可能在不改变绳长的情况下,通过调节绳子的连接点A、B、C、D的位置,使木块从木板的右端BD离开平台而维持细绳不断裂.(需必要的分析说明)
答案
(1)根据牛顿第二定律,有:
F-f=ma
即:7-2=1×a
解得:a=5m/s2
根据力矩平衡条件,有:
2T(0.5)=10×(
5t2)1 2
即:T=25t2
当T=25t2=9时绳子断开,解得:t=0.6s
(2)改变绳子与薄木板之间的夹角θ,从而增大拉力的力臂,绳长L为
,力臂d=L•cosθ•sinθ;2 3 3
当θ=45°时,dmax=3 3
∵10×1=2T3 3
T=8.66N<9N
∴可以通过调节绳子的连接,使物体有可能离开平台后做平抛运动;
答:(1)绳中的拉力T随时间t的变化规律如图所示;
(2)有可能在不改变绳长的情况下,通过调节绳子的连接点A、B、C、D的位置,使木块从木板的右端BD离开平台而维持细绳不断裂.
