问题
问答题
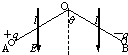
如图，质量均为m的两个小球A、B固定在弯成120°角的绝缘轻杆两端，OA和OB的长度均为l，可绕过O点且与纸面垂直的水平轴无摩擦转动，空气阻力不计．设A球带正电，B球带负电，电量均为q，处在竖直向下的匀强电场中．开始时，杆OB与竖直方向的夹角θ0=60°，由静止释放，摆动到θ=90°的位置时，系统处于平衡状态，求：
（1）匀强电场的场强大小E；
（2）系统由初位置运动到平衡位置，重力做的功Wg和静电力做的功We；
（3）B球在摆动到平衡位置时速度的大小v．
答案
（1）力矩平衡时：（mg-qE）l=（mg+qE）lsin（120°-90°），
即mg-qE=
（mg+qE），得：E=1 2
；mg 3q
（2）重力做功：Wg=mgl（cos30°-cos60°）-mglcos60°=（
-1）mgl3 2
静电力做功：We=qEl（cos30°-cos60°）+qElcos60°=
mgl3 6
（3）根据能量守恒定律，得
mv2=Wg+We=（1 2
-1）mgl，2 3 3
得小球的速度：v=
=△Ek m
．(
-1)gl2 3 3
答：（1）匀强电场的场强大小E为
；mg 3q
（2）系统由初位置运动到平衡位置，重力做的功Wg为（
-1）mgl，静电力做的功We为3 2
mgl．3 6
（3）B球在摆动到平衡位置时速度的大小v为v=
=△Ek m
．(
-1)gl2 3 3