问题
填空题
如图,倾角为θ的光滑斜面与光滑的半圆形轨道光滑连接于B点,固定在水平面上,在半圆轨道的最高点C装有压力传感器,整个轨道处在竖直平面内,一小球自斜面上距底端高度为H的某点A由静止释放,到达半圆最高点C时,被压力传感器感应,通过与之相连的计算机处理,可得出小球对C点的压力F,改变H的大小,仍将小球由静止释放,到达C点时得到不同的F值,将对应的F与H的值描绘在F-H图像中,如图所示,则由此可知( )

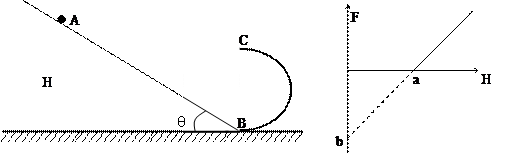
A 图线的斜率与小球的质量无关
B b点坐标的绝对值与物块的质量成正比。
C a的坐标与物块的质量无关。
D 只改变斜面倾角θ,a,b两点的坐标与均不变。
答案
BCD
小球由A到C的过程,由动能定理得 
在C点,由牛顿第二定律得 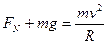
则牛顿第三定律得,压力传感器受到的压力大小F=FN
以上各式联立,可得 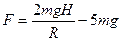
由此可知,图线的斜率为 且F=0时,H=2.5R,即a点坐标,
且F=0时,H=2.5R,即a点坐标,
b点的坐标为5mg,所以BCD正确,A错误。
