问题
问答题
设z=z(x，y)由方程sin2x+sin2y-z=ψ(x+y+z)所确定的函数，ψ有连续的二阶导数，且ψ＇≠1，
(Ⅰ) 求dz；
(Ⅱ) 记
答案
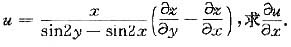
参考答案：[分析与求解] (Ⅰ) 对sin2x+sin2y-z=ψ(x+y+z)关于x求导[*]
同理可得[*]
所以[*]
或方程两边求全微分，由一阶全微分形式不变性得
dsin2x+dsin2y-dz=ψ2(x+y+z)d(x+y+z)
2sinxcosxdx+2sinycosydy-dz=ψ＇(x+y+z)(dx+dy+dz)
移项整理碍
(1+ψ＇)dz=(sin2x-ψ＇)dx+(sin2y-ψ＇)dy
[*]
dx与dy的系数分别[*]
(Ⅱ) [*]，代入u中，得
[*]
解析：[*]