问题
问答题
设f(x)是连续函数，且f(0)≠0，
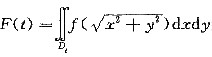，其中Dt=(x，y)x2+y2≤t2，t＞0。
(Ⅰ) 利用导数定义(不用变限积分求导公式)计算F＇(t)；
(Ⅱ) 证明：对于任意λ＞0，级数
收敛．
答案
参考答案：[分析与求解] [*]
根据导数定义，[*]
(Ⅱ) 由于F＇(t)=2πtf(t)，所以[*]
利用正项级数的比较判别法极限形式．
[*]
所以[*]绝对收敛，从而它是收敛的级数．