问题
问答题
设f(x)在(-∞,+∞)二阶可导,
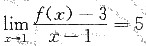 ,又f"(x)>0(x∈(-∞,+∞)),求证:
,又f"(x)>0(x∈(-∞,+∞)),求证:
f(x)>5x-2 (
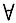 x≠1).
x≠1).
答案
参考答案:[分析与证明] 由
[*]
[证明1] (利用单调性证明不等式).
令 F(x)=f(x)-(5x-2) [*] F(1)=0
F'(x)=f'(x)-5, F'(1)=0
F"(x)=f"(x)>0([*]x)
[*]
即
f(x)>5x-2 ([*] x≠1).
[证明2] (利用微分中值定理证明不等式)
[*]
由微分中值定理得,存在ξ在x与1之间,
[*]
由f'(x)的单调上升性,当x<1时,由x<ξ<1 [*]
[*]
即
f(x)-f(1)>5(x-1)
当x>1时,由1<ξ<x [*]
[*]
即
f(x)-f(1)>5(x-1)
证明3 (利用凹凸性证明不等式)
y=f(x)在(-∞,+∞)是凹的. [*] 对[*]x,x0∈(-∞,+∞),x≠x0.
f(x)>f(x0)+f'(x0)(x-x0).
取x0=1得
f(x)>f(1)+f'(1)(x-1)=3+5(x-1)=5x-2.
