问题
问答题
求下列幂謦数的收敛区间及收敛域:
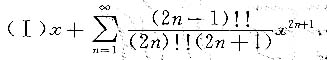
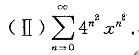
答案
参考答案:[分析与求解] (Ⅰ) 这里x的偶次方幂系数全为零.若将级数表为[*],则a2=0,于是[*]不存在,不能用求收敛半径公式.我们可用两种方法求收敛半径R.
[解法一] 每项提出公因子x,再令t=x2,并舍去第一项,得新的幂级数
[*]
相应的
[*]
[*] R=1.因t=x2,所以原幂级数的收敛半径R=1.收敛区间(-1,1).当x=±1时,原级数为
[*]
由于
[*]
可知此级数收敛,因此,原级数的收敛域为[-1,1].
[解法二] 将x看作任意取定的一个数,原级数就是数项级数
[*]
并有
[*]
[*] 当|x|<1时原级数收敛,当|x|>1时愿级数发散.因此,原级数的收敛半径R=1.
余下证明同解法一.
(Ⅱ) 记[*],有
[*]
因此,该幂级数的收敛半径[*].收敛区间是[*]
当x=±[*]时原级数分别为[*],均是发散的.因此收敛域为[*]
解析:[*]
