问题
问答题
设需求函数和总成本函数分别为P=a-bQ，
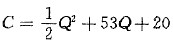，当需求Q对价格P的弹性
，收益R对产量Q的边
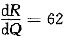时，其利润最大，
(Ⅰ) 求利润最大时的产量；
(Ⅱ) 确定a，b的值.
答案
参考答案：[分析与求解] 取得极值的必要条件是当利润函数L(Q)=R(Q)-C(Q)在Q0处取得极值时，则必有L＇(Q0)=0.即 R＇(Q0)=C＇(Q0)．利用此等式可求出利润最大时的产量．利用收益对Q的边际与需求对价格的弹性可求出a、b．
(Ⅰ) L(Q)=R(Q)-C(Q)，当利润最大时应有L＇(Q)=R＇(Q)-C＇(Q)=0，
即
[*]，因此，当Q=9时利润最大．
(Ⅱ) R(Q)=P(Q)·Q
[*]
将 [*]代入上式，得最大利润时的价格为P=73．
R(Q)=P(Q)·Q=aQ-bQ2
[*]
将Q=9，P=73.[*]代入①，②式得
[*]