问题
问答题
设
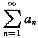 是正项级数,
是正项级数,
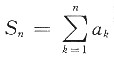 是它的部分和,求证:
是它的部分和,求证:
若
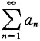 收敛,则
收敛,则
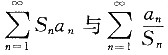 收敛.
收敛.
答案
参考答案:[分析与证明] 若正项级数[*]收敛,则部分和Sn有界:0<Sn≤M(n-1,2,3,…)[*]0<Snan≤Man
[*]收敛.同时因Sn单调上升[*] Sn≥S1=a1>0(n=1,2,3,…)
[*]
设
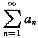 是正项级数,
是正项级数,
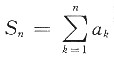 是它的部分和,求证:
是它的部分和,求证:
若
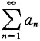 收敛,则
收敛,则
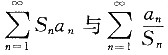 收敛.
收敛.
参考答案:[分析与证明] 若正项级数[*]收敛,则部分和Sn有界:0<Sn≤M(n-1,2,3,…)[*]0<Snan≤Man
[*]收敛.同时因Sn单调上升[*] Sn≥S1=a1>0(n=1,2,3,…)
[*]