问题
问答题
设a>0,证明不等式
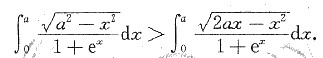
答案
参考答案:[分析与证明] 显然,无法直接计算不等式两边的定积分的值来进行比较.因此,需要利用定积分的性质等有关知识来判断.
[*]
则需证I>0,注意到
[*]
在X∈[0,a]上均表示[*]圆弧,但在[*]两侧
[*]
变号,因此将I的积分区间分为[*]
[*]
注意,当0<x<[*]时,0<x<a-x.于是上式积分中的被积函数当x∈(0,[*])时恒正,又被积函数在[0,[*]]连续,因此I>0.
解析:[*]
[*]
