问题
问答题
设x∈(0,1),证明不等式
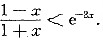
答案
参考答案:[分析与证明] [证法1]利用函数单调性.
将要证的不等式变形,(1-x)e2x<(1+x),x∈(0,1)
设f(x)=(1-x)e2x-(1+x),x∈(0,1)
则 f'(x)=(1-2x)e2x-1,f"(x)=-4xe2x,
当 x∈(0,1)时f"(x)<0.所以f'(x)单调递减,又f'(0)=0,因而f'(x)<0,从而f(x)单调递减.所以f(x)<f(0)=0,x∈(0,1)
即 (1-x)e2x-(1+x)<0,亦即[*]
[证法2] 要证的不等式等价于[*]
因
[*]
而 [*]
①式的一般项为2xn,②式一般项为[*],显然[*],当n≥3时,[*],所以当,n≥3,x∈(0,1)时[*],从而[*]即[*],亦即[*]
解析:[评注] (1)把要证明的不等式经过适当的变形有时可简化证明.
(2)利用函数单调性证明不等式的一般方法是先根据要证的不等式构造合适的辅助函数f(x),利用f'(x)在有关区间上的符号确定f(x)的单调性,再根据f(x)在有关点的值进一步确定f(X)的符号.
