问题
问答题
求
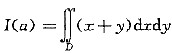，其中D由直线x=a，x=0，y=a，y=-a及曲线x2+y2=ax，(a＞0)所围．
答案
参考答案：[分析与求解] I(a)的积分区域如图阴影部分，设D1为由x=a，x=0，y=a，[*]所围．
[*]
由于D关于x轴对称，
故
[*]
[解法1] 将D1看成正方形区域与半圆形区域的差集，在半圆形区域上用极坐标变换．于是
[*]
于是
[*]
解析：[评注] 如果积分区域关于x轴(或y轴)对称，考察被积函数关于y(或x)奇偶性，往往会简化计算.
[解法2] 在直角坐标系下计算[*]
[*]
而
[*]
或
[*]
因此
[*]
[解法3] 被积函数x对x是奇函数，但积分区域D1关于y轴不对称，但关于x=[*]对称．作平移变换： [*]，v=y，则D1变为：
[*]
它关于v轴对称，于是
[*]
[*]