问题
问答题
(Ⅰ) 求定积分
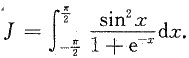
(Ⅱ) 设f(x)是可导函数,
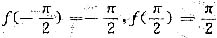 ,g(x)是f(x)的反函数,且满足
,g(x)是f(x)的反函数,且满足
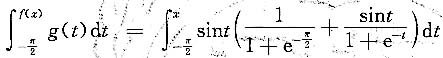 ,求积分
,求积分
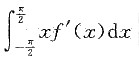 与
与
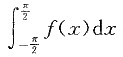 的值.
的值.
答案
参考答案:[分析与求解] [*],在此积分中令x=-t,
[*]
定积分的值与积分变量用什么字母表示无关,因此I可写为
[*]
于是
[*]
从而
[*]
由题[*]
(Ⅱ) 对[*]两边求导,得
[*]
因g(x)是f(x)的反函数,所以g[f(x)]=x,上式成为
[*]
两边在[*]上积分,
[*]
因[*]是奇函数,所以[*]
因为
[*]
所以有
[*]
